L1 Loss
又称L1范数损失、最小绝对值偏差(LAD)损失、最小绝对值误差(LAE)损失、平均绝对误差(Mean Absolute Error, MAE)损失。
表示模型预测值$f(x)$与真实值$y$之间距离的均值。
\[loss(x,y) = \frac{1}{n}\sum_{n=1}^{n}{|f(x_i)-y_i|}\]特点:
- 大部分情况下梯度也相等,对于小的损失值,梯度也很大,不利于函数的收敛
- 对于离群点不敏感
L2 Loss
又称L2范数损失、最小均方值偏差(LSD)损失、最小均方值误差(LSE)损失、平均均方误差(Mean Square Error, MSE)损失。
表示模型预测值$f(x)$与真实值$y$之间距离的平方的均值。
\[loss(x,y) = \frac{1}{n}\sum_{n=1}^{n}{(f(x_i)-y_i)^2}\]特点:
- 光滑连续、处处可导,随着误差的减小,梯度也在减小,有利于收敛到最小值
- 对离群点较为敏感
Smooth L1 Loss
\[smoothL_1(x) = \begin{cases} 0.5(f(x_i)-y_i)^2 & |x| < 1\\ |f(x_i)-y_i| - 0.5 & |x| \ge 1 \end{cases}\]特点:
- Smooth L1在 0 点可导
- 相比于L1损失函数,可以收敛得更快。相比于L2损失函数,对离群点、异常值不敏感,梯度变化相对更小
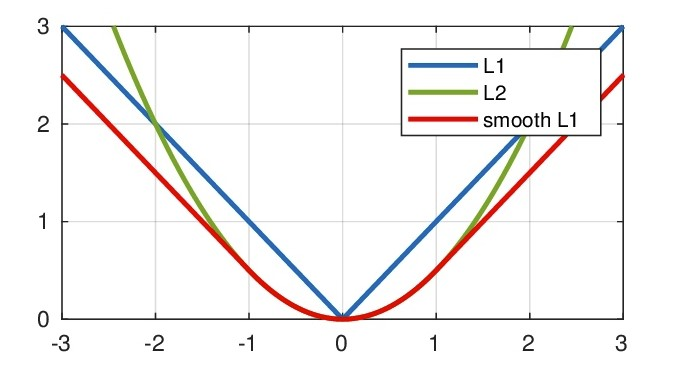
曲线