图像生成任务的几种架构
图像生成任务的困难在于:缺乏有效的指导,生成任务没有一个标准答案。
几种用于生成任务的神经网络架构:
-
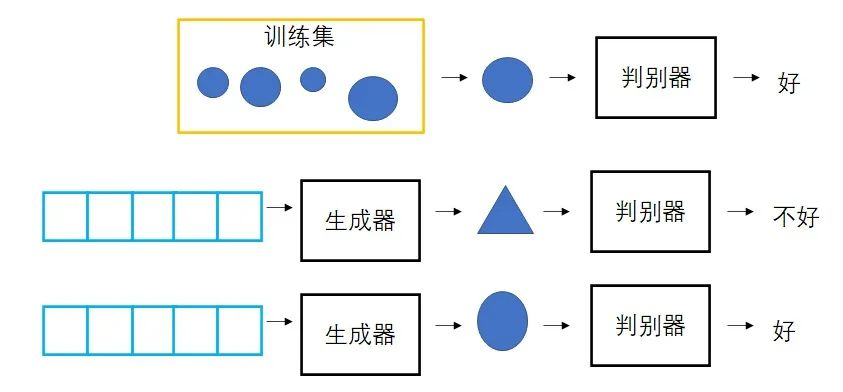
生成对抗模型 GAN
额外训练一个判别器用于判别生成图像是否和训练集中图片一样。
-
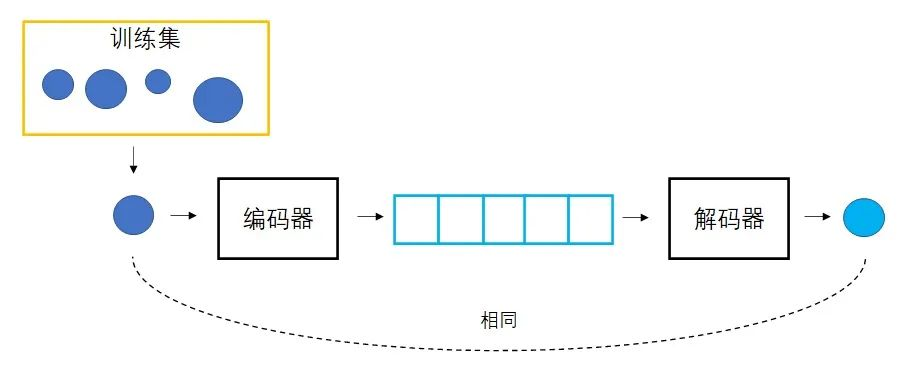
变分自编码器 VAE
学习向量生成图像的同时,也学习图像生成向量。图像变成向量,再用该向量生成图像,就应该能得到和原图一模一样的图像,每个向量的生成结果有了一个标准答案,从而可以指导网络训练。
-
扩散模型 Diffsion Model
一种特殊的 VAE,区别在于:
1)不再训练一个可学习的编码器,而是将编码过程固定成不断添加噪声的过程。
2)不再把图像压缩成更短的向量,自始至终都对一个等大的图像做操作,编解码的过程变成了加噪和去噪。
具体而言,扩散模型由正向过程和反向过程两部分组成,正向过程中,输入\(\mathbf{x}_0\)不断混入高斯噪声,经过\(T\)次加噪声操作后,图像\(\mathbf{x}_T\)会变成一幅符合标准正态分布的纯噪声图像;反向过程中,希望训练出一个神经网络,该网络能够学会\(T\)个去噪声操作,把\(\mathbf{x}_T\)还原为\(\mathbf{x}_0\)。网络的学习目标是让\(T\)个去噪声操作正好抵消掉加噪声操作。训练完毕后,只需要从标准正态分布中随机采样出一个噪声,再利用反向过程中的神经网络将该噪声恢复成一幅图像,就可以生成一幅图片。
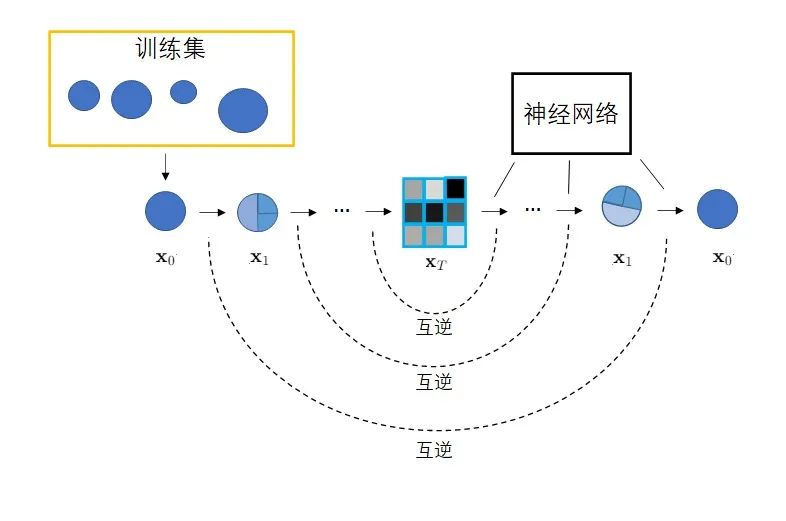
扩散模型的具体算法
前向过程
“加噪声”并不是给上一时刻的图像加上噪声值,而是从一个均值与上一时刻图像相关的生态分布中采样出一个新的图像。如下公式所示,其中\(\mathbf{x}_{t-1}\)是上一时刻的图像,\(\mathbf{x}_t\)是这一时刻的图像,而\(\mathbf{x}_t\)是从一个均值与\(\mathbf{x}_{t-1}\)有关的正态分布中采样得到的。因为\(\mathbf{x}_t\)只有\(\mathbf{x}_{t-1}\)决定,因此前向过程是一个马尔可夫过程。
\[\mathbf{x}_t \sim \mathcal{N}(\mu(\mathbf{x}_{t-1}),\sigma_t^2\mathbf{I} )\]绝大多数扩散模型会将这个正态分布设置成如下形式:
\[\mathbf{x}_t \sim \mathcal{N}(\sqrt{1-\beta_t}\mathbf{x}_{t-1}, \beta_t\mathbf{I})\]推导过程:
给定\(\mathbf{x}_0\),也就是从训练集中选取一幅图片,如何计算任意一个时刻\(t\)的噪声图像\(\mathbf{x}_t\)?
倒推,发现\(\mathbf{x}_t\)可以通过一个标准正态分布的样本\(\epsilon_{t-1}\)计算:
\[\begin{aligned} &\mathbf{x}_t \sim \mathcal{N}(\sqrt{1-\beta_t}\mathbf{x}_{t-1}, \beta_t\mathbf{I}) \\ \Rightarrow &\mathbf{x}_t = \sqrt{1-\beta_t}\mathbf{x}_{t-1} + \sqrt{\beta_t}\epsilon_{t-1};\epsilon _{t-1} \sim \mathcal{N}(0,\mathbf{I} ) \end{aligned}\]再往前推几步:
\[\begin{aligned} \mathbf{x}_t &= \sqrt{1-\beta_t}\mathbf{x}_{t-1} + \sqrt{\beta_t}\epsilon_{t-1} \\ &= \sqrt{1-\beta_{t}}(\sqrt{1-\beta_{t-1}}\mathbf{x}_{t-2} + \sqrt{\beta_{t-1}}\epsilon_{t-2}) + \sqrt{\beta_t}\epsilon_{t-1} \\ &= \sqrt{(1-\beta_{t})({1-\beta_{t-1}})}\mathbf{x}_{t-2} + \sqrt{(1-\beta_{t})\beta_{t-1}}\epsilon_{t-2}) + \sqrt{\beta_t}\epsilon_{t-1} \end{aligned}\]由正态分布的性质,均值相同的正态分布加到一起后,方差也会加到一起,也即\(\mathcal{N}(0,\sigma_1^{2}\mathit{I})\)与\(\mathcal{N}(0,\sigma_2^{2}\mathit{I})\)合起来会得到\(\mathcal{N}(0,(\sigma_1^{2} + \sigma_2^{2})\mathit{I})\),因此上式可化简为:
\[\begin{aligned} \mathbf{x}_t &= \sqrt{(1-\beta_{t})({1-\beta_{t-1}})}\mathbf{x}_{t-2} + \sqrt{(1-\beta_{t})\beta_{t-1}}\epsilon_{t-2}) + \sqrt{\beta_t}\epsilon_{t-1} \\ &= \sqrt{(1-\beta_{t})({1-\beta_{t-1}})}\mathbf{x}_{t-2} + \sqrt{(1-\beta_t)\beta_{t-1} + \beta_t}\epsilon \\ &= \sqrt{(1-\beta_{t})({1-\beta_{t-1}})}\mathbf{x}_{t-2} + \sqrt{1- (1-\beta_t)(1-\beta_{t-1})}\epsilon \end{aligned}\]继续往前推一步,可得到:
\[\begin{aligned} \mathbf{x}_t &= \sqrt{(1-\beta_{t})({1-\beta_{t-1}})({1-\beta_{t-2}})}\mathbf{x}_{t-3} + \sqrt{1- (1-\beta_t)(1-\beta_{t-1})({1-\beta_{t-2}})}\epsilon \end{aligned}\]由此,可以将公式一直推到\(\mathbf{x}_0\),令\(\alpha_t = 1 - \beta_{t}\),\(\bar\alpha_t = {\textstyle \prod_{i=1}^{t}}\alpha_i\),则: \(\mathbf{x}_t = \sqrt{\bar\alpha_t}\mathbf{x}_0 + \sqrt{1-\bar\alpha_t}\epsilon\)
所以,加噪声的公式可以是\(\mathbf{x}_t \sim \mathcal{N}(\sqrt{1-\beta_t}\mathbf{x}_{t-1}, \beta_t\mathbf{I})\),公式中\(\beta_t\)是一个小于1的常数,DDPM的论文中,\(\beta_t\)从\(\beta_1=10^{-4}\)线性增长到\(\beta_T=0.02\),\(\beta_t\)变大,\(\alpha_t\)越小,\(\bar\alpha_t\)趋于0的速度就越快,因此\(\mathbf{x}_T = \sqrt{\bar\alpha_T}\mathbf{x}_0 + \sqrt{1-\bar\alpha_T}\epsilon\)就就可以满足正态分布。
上述推断可以简单描述为:加噪声公式能够从慢到快的改变原图像,使图像最终均值为0,方差为\(\mathbf{I}\)。
反向过程
反向过程中,我们希望能够倒过来取消每一步加噪声的操作,让一幅纯噪声图像变回数据集中的图像。利用这个去噪声的过程,从而可以把任意一个从标准正态分布中采样出来的噪声图像变成一幅和训练数据差不多的图像,从而达到图像生成的目的。
当\(\beta_t\)足够小时,每一步加噪声的逆操作也满足正态分布,如下式所示,其中,当前时刻加噪声逆操作的均值\(\bar\mu_t\)和方差\(\bar\beta_t\)由当前时刻\(t\)和当前图像\(\mathbf{x}_t\)决定。
\[\mathbf{x}_{t-1} \sim \mathcal{N}(\bar\mu_t, \bar\beta_{t}\mathbf{I})\]因此,为了描述所有去噪声的操作,神经网络应该输入\(t\)和\(\mathbf{x}_t\),拟合当前的均值\(\bar\mu_t\)和方差\(\bar\beta_t\)。
注意:请区分去噪声和加噪声的逆操作,加噪声是固定的,加噪声的逆操作也是固定的。理想情况下,我们希望去噪声操作就等于加噪声逆操作。然而,加噪声的逆操作不太可能从理论上求得,只能由神经网络去拟合它。去噪声和加噪声逆操作的关系,相当于神经网络的预测值和真值的关系。
现在的问题是:加噪声逆操作的均值和方差是什么?如果给定训练集的输入\(\mathbf{x}_0\),加噪声逆操作的分布可以通过贝叶斯公式计算得到:
\[q(\mathbf{x}_{t-1}\mid \mathbf{x}_t,\mathbf{x}_0) = q(\mathbf{x}_t\mid \mathbf{x}_{t-1},\mathbf{x}_0)\frac{q(\mathbf{x}_{t-1}\mid \mathbf{x}_0)}{q(\mathbf{x}_t\mid \mathbf{x}_0)}\]等式左边表示加噪声的逆操作,表示已知\(\mathbf{x}_t\)和\(\mathbf{x}_0\)情况下下\(\mathbf{x}_{t-1}\)的概率分布,它的均值和方差都是待求的。右边是加噪声的分布。由于\(\mathbf{x}_0\)已知,\(q(\mathbf{x}_{t-1}\mid \mathbf{x}_0)\)和\(q(\mathbf{x}_t\mid \mathbf{x}_0)\)两项可以根据前面的公式\(\mathbf{x}_t = \sqrt{\bar\alpha_t}\mathbf{x}_0 + \sqrt{1-\bar\alpha_t}\epsilon_t\)得到:
\[\begin{aligned} q(\mathbf{x_t}\mid \mathbf{x_0}) &= \mathcal{N}(\mathbf{x}_t; \sqrt{\bar\alpha_t}\mathbf{x}_0,(1-\bar\alpha_t)\mathbf{I}) \\ q(\mathbf{x_{t-1}}\mid \mathbf{x_0}) &= \mathcal{N}(\mathbf{x}_{t-1}; \sqrt{\bar\alpha_{t-1}}\mathbf{x}_0,(1-\bar\alpha_{t-1})\mathbf{I}) \\ \end{aligned}\]将这两式代入上式等号右边,并带入贝叶斯公式得到:
\[\begin{aligned} q(\mathbf{x_{t-1}}\mid \mathbf{x_t},\mathbf{x_0}) = &\frac{1}{\beta_t\sqrt{2\pi}} exp(-\frac{(\mathbf{x}_t-\sqrt{1-\beta_t}\mathbf{x}_{t-1})^2}{2\beta_t})\cdot{} \\ &\frac{1}{(1-\bar\alpha_{t-1})\sqrt{2\pi}}exp(-\frac{(\mathbf{x}_{t-1}-\sqrt{\bar\alpha_{t-1}}\mathbf{x}_0)^2}{2(1-\bar\alpha_{t-1})})\cdot{} \\ &(\frac{1}{(1-\bar\alpha_{t})\sqrt{2\pi}}exp(-\frac{(\mathbf{x}_{t-1}-\sqrt{\bar\alpha_{t}}\mathbf{x}_0)^2}{2(1-\bar\alpha_{t})}))^{-1} \\ \end{aligned}\]由于多个正态分布的乘积还是正态分布,所以有:
\[\begin{aligned} q(\mathbf{x_{t-1}}\mid\mathbf{x_t},\mathbf{x_0}) = \frac{1}{\tilde{\beta}_t \sqrt{2\pi}}exp(-\frac{(\mathbf{x}_{t-1}-\tilde\mu)^2}{2\tilde\beta_t}) \end{aligned}\]所以现在求\(q(\mathbf{x_{t-1}}\mid\mathbf{x_t},\mathbf{x_0}) = \mathcal{N}(\mathbf{x}_{t-1};\tilde\mu_t,\tilde\beta_t\mathbf{I})\)的均值和方差:
方差可以通过指数函数的系数得到,系数为:
\[\begin{aligned} &\frac{1}{\beta_t\sqrt{2\pi}} \cdot \frac{1}{(1-\bar\alpha_{t-1})\sqrt{2\pi}} \cdot (\frac{1}{(1-\bar\alpha_{t})\sqrt{2\pi}})^{-1} \\ = &\frac{(1-\bar\alpha_t)}{\beta_t(1-\bar\alpha_{t-1})\sqrt{2\pi}} \end{aligned}\]所以,最终的方差为:
\[\begin{aligned} \tilde\beta_t = \frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t} \cdot \beta_t \end{aligned}\]接下来关注指数部分,指数部分是关于\(\mathbf{x}_{t-1}\)的二次函数,只需要化简成\((\mathbf{x}_{t-1}-C)^2\)的形式,再除以\(-2\)倍方差,就可以得到均值。
指数部分为:
\[\begin{aligned} -\frac{1}{2}(\frac{(\mathbf{x}_t-\sqrt{1-\beta_t}\mathbf{x}_{t-1})^2}{\beta_t} +\frac{(\mathbf{x}_{t-1}-\sqrt{\bar\alpha_{t-1}}\mathbf{x}_0)^2}{(1-\bar\alpha_{t-1})} -\frac{(\mathbf{x}_{t-1}-\sqrt{\bar\alpha_{t}}\mathbf{x}_0)^2}{(1-\bar\alpha_{t})}) \end{aligned}\]把和\(\mathbf{x}_{t-1}\)有关的项计算化简,可以计算出均值:
\[\tilde\mu_t = \frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}\mathbf{x}_t + \frac{\sqrt{\alpha_{t-1}}\beta_t}{1-\bar\alpha_t}\mathbf{x}_0\]上式中,\(\mathbf{x}_t\)已知,\(\mathbf{x}_0\)未知,而\(\mathbf{x}_t\)是\(\mathbf{x}_0\)在正向过程中第\(t\)步加噪声的结果,根据正向公式倒推:
\[\begin{aligned} &\mathbf{x}_t = \sqrt{\bar\alpha_t}\mathbf{x}_0 + \sqrt{1-\bar\alpha_t}\epsilon_t \\ &\mathbf{x}_0 = \frac{\mathbf{x}_t-\sqrt{1-\bar\alpha_t}\epsilon_t}{\sqrt{\bar\alpha_t}} \end{aligned}\]将\(\mathbf{x}_0\)带入上述公式,可以得到最终的均值:
\[\tilde\mu = \frac{1}{\sqrt{\alpha_t}}(\mathbf{x}_t - \frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}}\epsilon_t)\]注意,\(\beta_t\)是加噪声的方差,是一个常量,所以加噪声逆操作的方差\(\tilde\beta_t\)也是一个常量,因此在训练去噪网络时,神经网络只用拟合\(T\)个均值,而不用拟合方差。
训练神经网络的最后一步是如何设置训练的损失函数,加噪声逆操作和去噪声操作都是正态分布,网络训练目标是让每对正态分布更加接近,也就是让两个正态分布的均值和方差都尽可能接近,而方差是常量,只用让均值尽可能接近就可以了。
又由计算均值的公式可得,式中只有一个未知量\(\epsilon_t\),因此预测均值等同于预测噪声\(\epsilon_\theta(\mathbf{x}_t,t)\),其中\(\theta\)为可学习参数,让它与生成\(\mathbf{x}_t\)的噪声\(\epsilon_t\)的均方误差最小即可,所以最终的误差函数可以写成 \(L = \parallel \epsilon_t - \epsilon_\theta(\mathbf{x}_t,t)\parallel ^2\)
总结:反向过程中,神经网络应该让\(T\)个去噪声操作拟合对应的\(T\)个加噪声逆操作,每步加噪声逆操作符合正态分布,且在给定的某个输入时,该正态分布的均值和方差可以用解释式表达。因此,神经网络的学习目标是让其输出的去噪声分布和理论计算的加噪声逆操作分布一致,并经过推导简化,问题转换为拟合生成\(\mathbf{x}_t\)时用到的随机噪声\(\epsilon_t\)。
训练算法和采样算法
以下为 DDPM 论文中的训练算法:

第二行:从训练集中取一个数据\(\mathbf{x}_0\)
第三行:随机从\(1,...,T\)中取一个时刻用来训练,虽然要求神经网络拟合\(T\)个正态分布,但实际训练时,不用一轮预测\(T\)个结果,只需要随机预测\(T\)个时刻中某一个时刻的结果
第四行:生成一个噪声\(\epsilon\),用于执行前向过程生成\(\mathbf{x}_t = \sqrt{\bar\alpha}\mathbf{x}_0 + \sqrt{1-\bar\alpha_t}\epsilon\),之后将\(\mathbf{x}_t\)和\(t\)传给神经网络\(\epsilon_\theta(\mathbf{x}_t,t)\),让网络预测随机噪声。损失函数是预测噪声与实际噪声之间的均方误差
第五行:采用随机梯度下降优化网络
采样算法:

第一行:从标准正态分布中随机采样的输入噪声\(\mathbf{x}_T\)
第二到四行:令时刻从\(T\)到\(1\),计算这一时刻去噪声操作的均值和方差,并采样出\(\mathbf{x}_{t-1}\),循环执行去噪声操作,最后生成的\(\mathbf{x}_0\)就是生成的图像。