一、概述
SLAM(Simultaneous Localization and Mapping),同时定位与地图构建。指搭载特定传感器的主体,在没有环境先验信息的情况下,于运动中建立环境的模型,同时估计自己的运动。
二、SLAM框架
1、传感器信息读取。相机图像信息读取与预处理。
2、前端视觉里程计(Visual Odometry)。估算相邻图像间相机的运动,以及局部地图的样子。
3、后端(非线性)优化。接受不同时刻视觉里程计测量的相机位姿,以及回环检测的信息,对它们进行优化,得到全局一致的轨迹和地图。
4、回环检测。判断机器人是否到达过先前的位置,如果检测到回环,会把信息提供给后端处理。
5、建图。根据估计的轨迹,建立与任务要求对应的地图。
三、三维空间刚体运动
欧氏空间坐标变化:旋转矩阵 R + 平移向量 t .
\[a^{\prime} = Ra+t\]旋转矩阵组成特殊正交群 SO(n):
\[SO(n) = \{ R \in \mathbb{R}^{n \times n} \mid RR^{T}=I,det(R)=1 \}\]其中,SO(3) 表示三维空间旋转。
转化为齐次坐标和变换矩阵 T 形式:
\[\begin{bmatrix} a^{\prime } \\ 1 \end{bmatrix} = \begin{bmatrix} R & t\\ 0^{T} & 1 \end{bmatrix} \begin{bmatrix} a \\ 1 \end{bmatrix} = T \begin{bmatrix} a \\ 1 \end{bmatrix}\]变换矩阵又称特殊欧氏群 SE(3):
\[SE(3) = \{ T = \begin{bmatrix} R & t \\ 0^{T} & 1\end{bmatrix} \in R^{4 \times 4 } \mid R \in SO(3), t \in \mathbb{R}^{3} \}\]总结:三维空间中,旋转由旋转矩阵 SO(3) 描述,平移由 $\mathbb{R}^3$ 向量描述,将旋转与平移放入一个矩阵中,形成变换矩阵 SE(3) .
罗德里格斯公式
旋转向量转换到旋转矩阵:
\[R=\cos\theta I +(1-\cos\theta)nn^T+\sin\theta n^\wedge\]四元数
四元数:解决旋转矩阵的冗余性和欧拉角、旋转向量的奇异性。
一个四元数 q 表示为:
\[q = q_{0} + q_{1}i + q_{2}j + q_{3}k\]绕单位向量 $n=\begin{bmatrix} n_{x},n_{y},n_{z} \end{bmatrix}^T$ 旋转角度为 n ,得到旋转的四元数形式为:
\[n=\begin{bmatrix} cos{\frac{\theta}{2}}, n_{x}sin{\frac{\theta}{2}}, n_{y}sin{\frac{\theta}{2}}, n_{z}sin{\frac{\theta}{2}} \end{bmatrix}^T\]四元数对应的旋转矩阵 R 为:
\[R = \begin{bmatrix} 1-2q_2^2-2q_3^2 & 2q_1q_2-2q_0q_3 & 2q_1q_3+2q_0q_2 \\ 2q_1q_2+2q_0q_3 & 1-2q_1^2-2q_3^2 & 2q_2q_3-2q_0q_1 \\ 2q_1q_3-2q_0q_2 & 2q_2q_3+2q_0q_1 & 1-2q_1^2-2q_2^2 \end{bmatrix}\]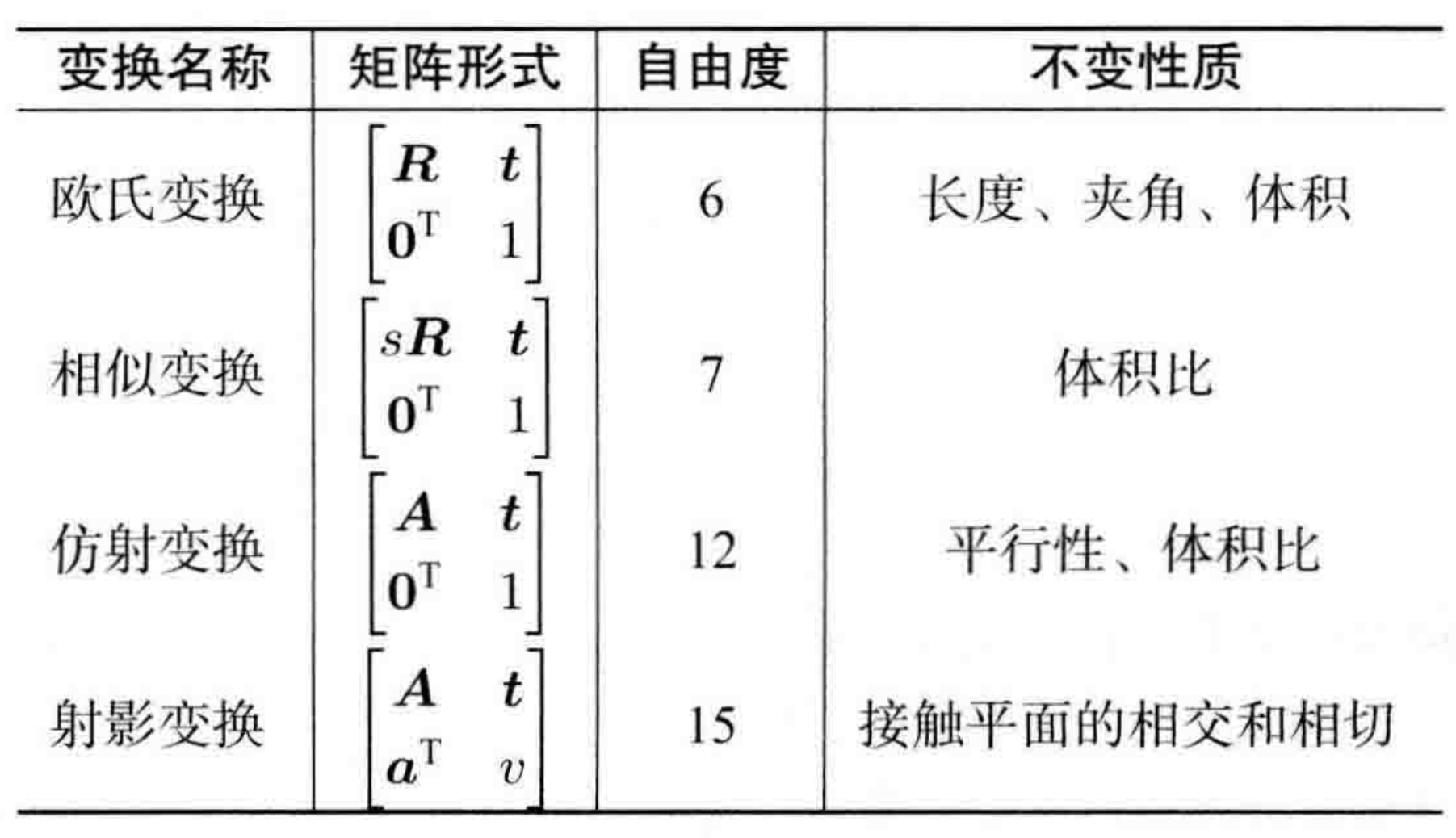
四、李群与李代数
群:一种集合加上一种运算的代数结构。具有封闭性、结合律、幺元、逆的性质。
李群:具有连续(光滑)性质的群。这里主要指 SO(3) 和 SE(3) .
李代数:每个李群都有与之对应的李代数,用于描述李群的局部性质。具有封闭性、双线性、自反性、雅可比等价的性质。
李代数 $\mathfrak{so}(3)$
$\mathfrak{so}(3)$ 是由三维向量组成的集合,每个向量对应一个反对称矩阵,表示旋转矩阵的导数。
\[\mathfrak{so}(3) = \{ \phi \in \mathbb{R}^3, \Phi=\phi^{\wedge} \in \mathbb{R}^{3 \times 3} \}\]李代数 $\mathfrak{se}(3)$
\[\mathfrak{se}(3) = \{ \xi=\begin{bmatrix} \rho \\ \phi \end{bmatrix} \in \mathbb{R}^6, \rho \in \mathbb{R}^3, \phi \in \mathfrak{so}(3), \xi^{\wedge}=\begin{bmatrix} \phi^\wedge & \rho \\ 0^T & 0 \end{bmatrix} \in \mathbb{R}^{4 \times 4} \}\]$\mathfrak{se}(3)$ 元素记作 $\xi$ ,是一个六维向量,前三维为平移,记作 $\rho$ ;后三维为旋转,记作 $\phi$ .
指对数映射
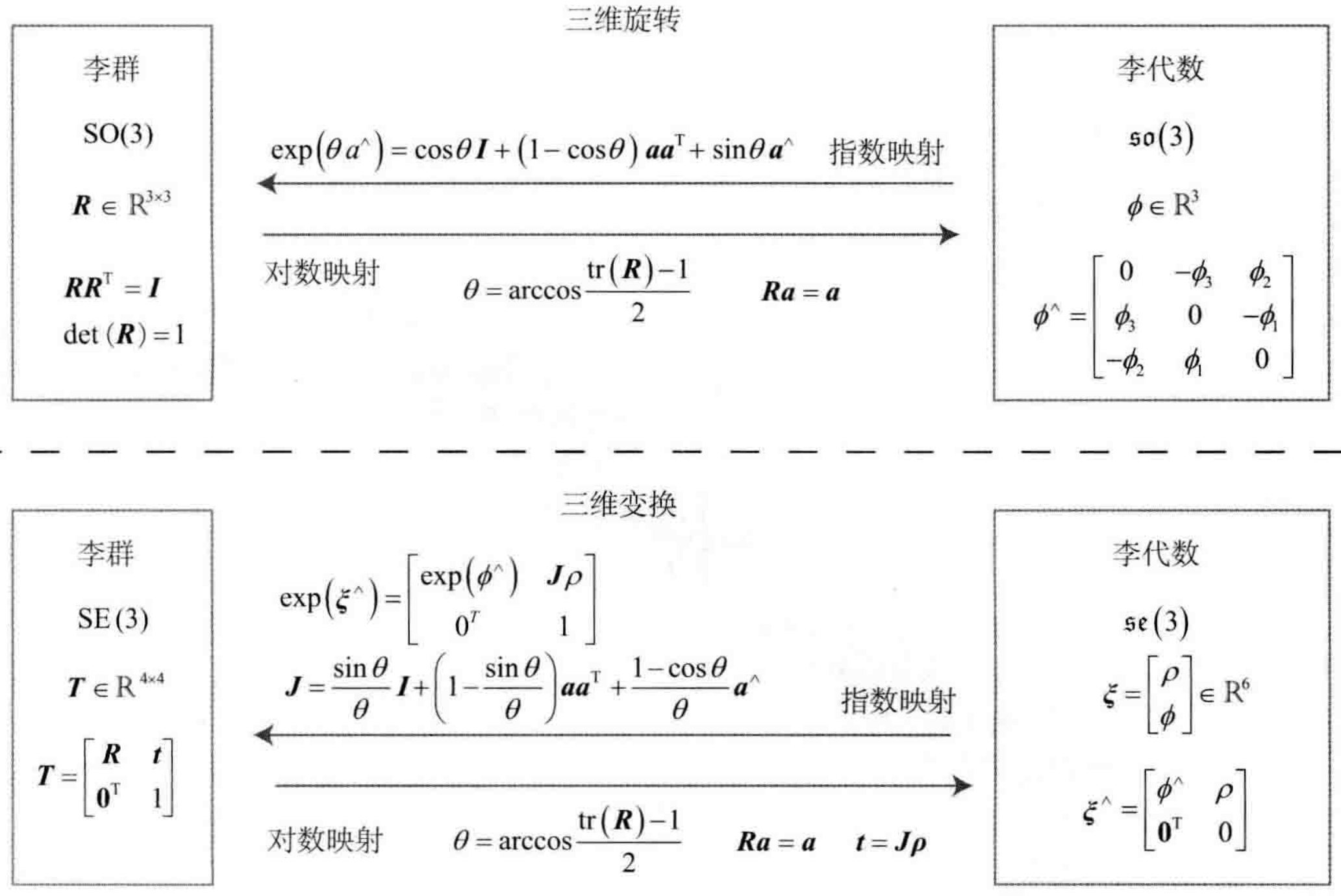
李代数求导与扰动模型
用到时补充。
五、相机图像
\[Z \begin{pmatrix} u \\ v \\ 1 \end{pmatrix} = \begin{pmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} X \\ Y \\ Z \end{pmatrix} = KP\]相机标定:确定相机的内参数K。
将P从相机坐标转换到世界坐标P_w: \(Z P_{uv}=Z\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = K(RP_w + t) = KTP_w\)
相机位姿:相机的外参数 R 和 t .
六、非线性优化
高斯牛顿法
列文伯格-马夸尔特方法
七、视觉里程计
特征点法
特征提取:SIFT、SURF、ORB 特征匹配:快速近似最近邻(FLANN) 相机运动估计:2D-2D对级几何、3D-2DPnP、3D-3DICP
直接法
光流:Lucas-Kanade稀疏光流,用于跟踪特征点位置。
八、后端
卡尔曼滤波
Bundle Adjustment 图优化
BA:带有相机位姿和空间点的图优化。
Pose Graph 优化
PG:不优化路标点的位置,只关心相机位姿。